SPSS 散点图与拟合线工具
作者：Ruben Geert van den Berg，发布于 SPSS Tools 和 Regression
目录
- 示例数据文件
- 前提条件与安装
- 示例 I - 创建所有独特的散点图
- 示例 II - 预测变量的线性度检查
可视化你的数据是对数据进行处理的最好方法之一。这样做可能只需要一点努力：在 SPSS 中，只需一行 FREQUENCIES 命令就可以一次性创建多个直方图或条形图。
遗憾的是，散点图的情况有所不同：每个散点图都需要单独的命令。因此，我们构建了一个工具，用于创建一组变量之间的一个、多个或所有散点图，可以选择带有（非）线性拟合线和回归表。
示例数据文件
在本教程中，我们将使用 health-costs.sav（部分如下图所示）。
我们鼓励你下载并打开此文件，并复现我们将在稍后展示的示例。
前提条件与安装
我们的工具需要 SPSS 24 或更高版本。此外，必须安装 SPSS Python 3 essentials（通常是最新 SPSS 版本的情况）。
点击 SPSS_TUTORIALS_SCATTERS.spe 下载我们的散点图工具。你可以通过“扩展 (E x tensions)” 
“安装本地扩展包 (I nstall local extension bundle)”来安装它，如下所示。
在打开的对话框中，导航到下载的 .spe 文件并安装它。SPSS 将确认扩展已成功安装在“图形 (G r aphs)” “SPSS tutorials - Create All Scatterplots”下。
示例 I - 创建所有独特的散点图
现在，让我们检查健康成本（health costs）、酒精（alcohol）和香烟（cigarette）消费以及锻炼（exercise）之间所有独特的散点图。我们将导航到“图形 (G r aphs)” “SPSS tutorials - Create All Scatterplots”，并填写如下所示的对话框。
我们将所有相关变量作为 y 轴变量输入。我们建议你始终首先输入因变量（如果存在）。
我们将这些相同的变量作为 x 轴变量输入。
y 轴和 x 轴变量的这种组合会导致重复的图表。例如，成本与酒精（costs by alco）类似于酒精与成本（alco by costs）的转置。如果选择“仅分析 y,x 并跳过 x,y（analyze only y,x and skip x,y）”，则会跳过此类重复项。
除了创建散点图外，我们还将快速浏览生成的 SPSS 语法 (syntax)。
如果未输入标题，我们的工具将应用自动标题。对于此示例，自动标题相当冗长。因此，我们使用所有图表的固定标题（“散点图（Scatterplot）”）覆盖它们。完全没有标题的唯一方法是使用图表模板来抑制它们。
点击“粘贴 (P aste)”会生成以下语法。让我们运行它。
SPSS 散点图工具 - 语法 I
***创建成本、酒精、香烟和锻炼之间所有独特的散点图。
**
SPSS TUTORIALS SCATTERS YVARS=costs alco cigs exer XVARS=costs alco cigs exer
/OPTIONS ANALYSIS=SCATTERS ACTION=BOTH TITLE="Scatterplot" SUBTITLE="All Respondents | N = 525".结果
首先，请注意，我们的工具运行的 GRAPH 命令也已打印在输出窗口中（如下所示）。你可以复制、粘贴、编辑并在任何 SPSS 安装上运行这些命令，即使它没有安装我们的工具。
在此语法下，我们找到了所有 6 个独特的散点图。它们中的大多数显示了实质性的 相关性 (correlations)，并且它们看起来都是合理的。但是，请注意，一些图（尤其是第一个）暗示了一些曲线关系（curvilinearity）。我们将在第二个例子中彻底调查这一点。
无论如何，我们认为在进行 SPSS 相关分析 (SPSS correlation analysis) 之前，快速查看此类散点图应该始终进行。
示例 II - 预测变量的线性度检查
我现在想运行一个 多元回归分析 (multiple regression analysis)，以从几个预测变量预测健康成本。但在这样做之前，让我们看看每个预测变量是否与我们的因变量呈线性关系。再次，我们导航到“图形 (G r aphs)” “SPSS tutorials - Create All Scatterplots”，并填写如下所示的对话框。
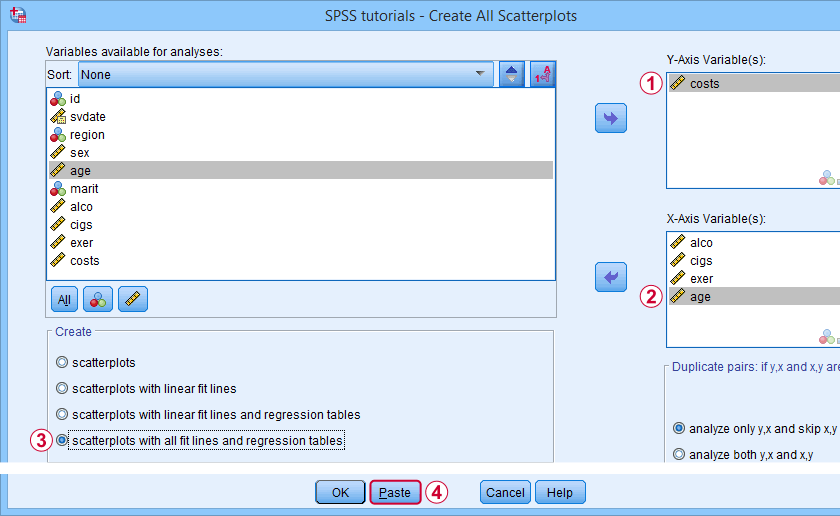
我们的因变量（dependent variable）是我们的 y 轴变量。
所有自变量（independent variable）都是 x 轴变量。
我们将创建带有所有拟合线（all fit lines）和回归表（regression tables）的散点图。
点击“粘贴 (P aste)”按钮后，我们将运行以下语法。
SPSS 散点图工具 - 语法 II
***将 4 个预测变量的所有可能曲线拟合到单个因变量上。
**
SPSS TUTORIALS SCATTERS YVARS=costs XVARS=alco cigs exer age
/OPTIONS ANALYSIS=FITALLTABLES ACTION=RUN.请注意，运行此语法会触发一些关于某些变量中零值的警告（warnings）。对于这些示例，可以安全地忽略这些警告。
结果
在我们的第一个带有 回归线 (regression lines) 的散点图中，如下所示，一些曲线与线性度显着偏差。
遗憾的是，此图表的图例（legend）无法帮助识别哪个曲线可视化哪个转换函数（transformation function）。因此，让我们看一下如下所示的回归表。
非常有趣的是，当我们将平方预测变量添加到我们的模型中时，r 平方（r-square）从 0.138 急剧上升到 0.200。b 系数（b-coefficients）告诉我们，该模型的回归方程是“成本（Costs）’ = 4,246.22 - 55.597 * 酒精（alco）+ 6.273 * 酒精（alco）2”。不幸的是，此表不包括这些 b 系数的显着性水平（significance levels）或 置信区间 (confidence intervals)。但是，在将平方预测变量添加到我们的数据之后，可以很容易地从回归分析中获得这些值。以下语法就是这样做的。
***计算平方酒精消费量。
**
compute alco2 = alco**2.
***成本对平方和非平方酒精消费量的多元回归。
**
regression
/statistics r coeff ci(95)
/dependent costs
/method enter alco alco2.结果
首先请注意，我们复制了我们之前看到的完全相同的 b 系数。
令人惊讶的是，我们的平方预测变量比其原始的非平方对应物更具 统计显着性 (statistically significant)。
Beta 系数（beta coefficients）表明平方预测变量的相对强度大约是原始预测变量的 3 倍。
简而言之，这些结果表明至少有一个预测变量存在显着的非线性。有趣的是，使用标准线性度检查无法检测到这一点：在运行多元回归后，检查标准化残差与预测值的散点图。
但无论如何，我只是想分享我为这些分析构建的工具，并用一些典型的例子来说明它。希望你觉得它有帮助！